I Am SO Glad I’m Uncoordinated!
Technology trends have evolved to provide an abundance of CPU, Memory, Storage, and Networking. Coordination, formerly dirt cheap, has become the precious commodity.
Sometime around 1962 or 1963, I was six or seven years old. I was trotted down to the Little League field and told I should sign up. It wasn’t too bad standing in the outfield until I understood they were SERIOUS that I should move into the path of the approaching ball! The odds of me lining up the mitt to the oncoming ball were vanishingly small. I lasted less than a week in Little League. So, I took up reading books and that’s served me well. I am truly glad that I’m uncoordinated!
In this paper, we’re going to look at how computing has evolved through the years. The act of coordinating to share stuff hurts more and more over time. We’ll first examine how this has changed and continues to change. Then, we’ll look at how we can reduce and sometimes eliminate these challenges over time.
The World Has Changed in 45 Years!
I’ve seen tremendous changes since I dropped out of college in 1976. The nature and character of our designs continue to evolve as technology advances. Stuff that used to be easy is now hard. Stuff that used to be hard is now easy.
The way we write data has begun an inexorable change from updating the single copy of some data to adding new versions to a log of changes. Similar to the way accountants only add journal entries, our systems are appending their intention to make changes to a log. This means the data we store is immutable. Being immutable means, it is more easily managed in a distributed environment, avoiding the difficulties of read-modify-write. Also, we can bundle appended log writes into one batched append.
The way we read data has similarly evolved. Immutable data can be unambiguously copied and cached. We grab larger and larger amounts of data, taking advantage of increasing bandwidth hoping to reduce the times we wait for missing information.
The biggest challenge, however, comes from the pain of coordinating with a distant partner. We may lose opportunities to do a lot of work as we sit around with our thumb-in-our-bum waiting to ensure we won’t get tangled up with a distant partner’s concurrent work. What makes coordination so hard?
Latching in My First Programming Job
In 1978, I was 22 years old. I started work at BTI Computer Systems building software for the BTI 8000. It was a SMP (Symmetric Multi-Processor) system with many CPUs accessing the same shared memory. It was not a common architecture at that time.
My friend, Glenn, and I were commissioned to write a database system for this machine. Memory, CPU, and storage were scarce and precious. They required obsessive care to optimize. Whenever we needed to access shared memory, we simply grabbed a semaphore ensuring we didn’t muck up our shared data. After reading some database papers, we started to call these “latches” while the crazy OS people down the hall called them “locks”.
Grabbing a latch was amazingly cheap. We were working on a very slow processor on a 20” x 23” printed circuit board with no cache. This plugged into a 16-slot backplane with other boards containing memory, peripheral access, and the system controller. With a 15MHz system clock, the 12 cycles to access memory could be completed in 750ns. Memory implemented latches. This supported coherent and coordinated access by up to 8 CPUs sharing the bus in the same time as reading or writing memory. Fortunately, the CPUs were so darned slow that we didn’t see contention for the shared bus. It worked pretty well to plug in more CPUs. Old benchmarks showed 5.5X throughput with 7 CPUs on the shared bus. See The BTI 8000 – Homogeneous, general purpose multiprocessing. My first foray into scalable computing!
40+ years ago, it was clear that:
CPU was expensive and precious
Memory was expensive and precious
Storage was expensive and precious
Network was infinitely expensive (as we had no network)
Coordination was close to free!
Our Current Challenges Are Exactly the Opposite of Our Old Ones!
Unlike the olden days, we continue to get more and more memory, persistent storage
(SSDs and NVMe), network bandwidth, and CPU. Hard disk drive (HDD) storage capacity continues to increase but it is getting colder (e.g., less access bandwidth relative to its capacity).
We have more stuff:
CPU processing and DRAM continue to grow in capacity (and drop in cost) roughly aligned with Moore’s Law (doubling every 2 years). The recent Apple M1 chip has 5nm technology and 16 billion transistors on a single chip! Wow!
SSD and NVMe persistent storage are also tracking Moore’s Law. In data centers, low latency logging is held in replicated storage servers (to tolerate loss of a server). This can be done in 1-10ms (over 3 nodes in a datacenter). Mostly, we use append-only logs to manage latency for durable writes.
Network bandwidth seems to track closely with Gilder’s Law (doubling every 6 months). 400Gb-ethernet is common. 1Tb-ethernet is here. It is typical to see intra-datacenter RPC over TCP in the 100-microsecond range. RDMA (Remote Direct Memory Access) is emerging with much lower latency by eliminating software in the path to move data across servers but it’s not widely used yet.
HDD is rapidly becoming archive storage. While the cost per GB of storage is dropping as the areal density of disks increase, the transfer rate is only rising with the linear density (or the square root of the areal density). Use of HDD is necessarily getting colder and more focused on archival.
With all these wonderful improvements, the amount of time waiting to get to something else has become the bottleneck. Latency is the design point.
Modern CPU chips have upwards of 8-10 complex and sophisticated cores. Some designs have over 100 simpler cores. These numbers continue to increase. They may have over 500 of out-of-order execution buffers usually waiting for memory. If all goes well, they commit 6-8 instructions per cycle. This is an amazing feat that only works when all the memory needed has been supplied. The demise of Dennard Scaling means chips get too hot when we run them faster. We are getting LOTS more circuitry as the transistor geometry shrinks but we can’t run the clocks faster. Consequently, we get a lot more parallel computation, more cores, more threads, and more theoretical max throughput from each socket. This, however, is all dependent on feeding the beast with data.
If the CPU needs a piece of memory and it’s not close by, we lose opportunities to do work. There may be other work to launch on another thread but changing threads takes time.
Let’s attempt to place the cost impact of latency into perspective. Consider the delays incurred as we read data that is not available to the core. The farther away the data resides, the more work opportunity we lose as we read the data.
These latencies consider the time required to read data. If you want to modify data and ensure it doesn’t get tangled up by someone else whacking on it at the same time, that may take much longer. A simple read followed by a compare-and-swap takes twice as long as these numbers, once to read and once to CAS. That’s assuming no one else is fighting with you for the update. Server-to-server RPCs can involve many more round trips, depending on how you coordinate your work with the remote server.
Doing a “blind write” (where you are slapping a value onto the memory location without looking first) typically takes a similar amount of time as reading. Hence, if we make updates by logging the desired new value, we may save time. Appending to a log can be implemented as a “blind write” and, if done with care, can support a pipelined sequence with MANY writes happening one after the other. Confirmation time still takes two round trips but a caravan of writes can push a lot of stuff in close to the time of a single round trip.
Some stuff is far away! Coordinating is usually double far away!
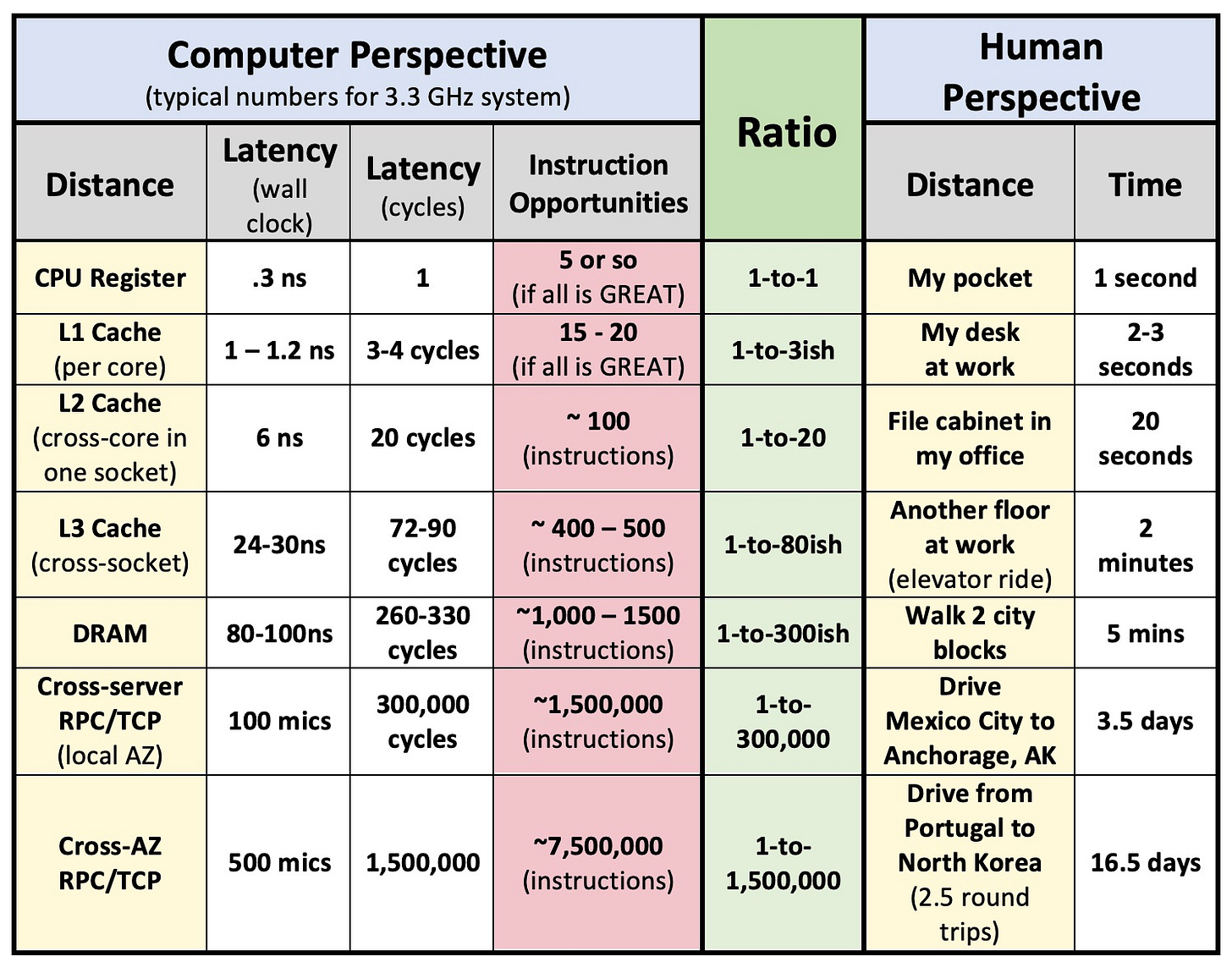
The following table is motivated by a graphic in the 1995 paper AlphaSort: A Cache-Sensitive Parallel External Sort by Chris Nyberg, Jim Gray et al. That paper shows the massive improvements possible to sorting algorithms as the system feeds the caches BEFORE the data is needed.
It’s striking to compare typical latencies within the 1995 Alpha to today’s typical latencies.
The time to for a CPU to access its CPU cache on the 150MHz Alpha box is about the same in terms of cycles.
The time to access DRAM in 1995 is the same in wall clock time (around 80ns) but 20 times as many cycles in a modern 3GHz machine.
If your modern machine is 4GHz, you see 27 times as many cycles to access DRAM since the cycles are faster.
Most things have been getting farther and farther away every year for more than 30 years!
Consider the following round-trip latencies and think about how much performance is lost each time you need distant data you don’t have.
So, it takes a long time to get there and back. How much data can you bring with you to avoid going back to get it? As network bandwidth increases, you can bring more and more along!
Clearly, data in CPU registers can be accessed 300 times as fast as data in DRAM. How about getting data from another server?? In the same datacenter, it typically takes 300,000 times as long to get something from another server as from your CPU register! Can you plan what you will need? Can you plan what you MIGHT need? If you need to get to another AZ (Availability Zone) in a cloud datacenter, you will probably wait more than 1,500,000 times as long as accessing it inside your CPU.
Heaven forbid you need to coordinate across these distances by doing a compare-and-swap to DRAM or, much worse, an update to Zookeeper. Both of these require a read followed by a compare-and-swap assuming you get lucky and don’t have to contend with another updater!
The challenges in computing continue to evolve!
Dave Patterson pointed out in the 2004 paper Latency lags bandwidth that we ARE getting lots more bandwidth but we AREN’T getting improvements to latency. His points in 2004 were true then and remain true 17 years later. It seems like this trend will continue.
For quite a while now (and for the foreseeable future), I see a dramatically different world than when I dropped out of college in the 1970s. As we design our solutions, we must consider:
CPU is cheap and getting cheaper
Memory is cheap and getting cheaper
Storage is cheap and getting cheaper
Network is cheap and getting cheaper
Coordination is the only remaining hard problem!
This dramatically inverts our systems as we try to minimize coordination by squandering CPU, memory, storage, and network bandwidth in our quest to avoid getting stuck coordinating.
Inverting How We Read Data
It used to be in the 1970s that we would be pretty careful to avoid unnecessarily reading data. CPU cache capacity was precious so we only grabbed something when it was pretty clear we needed it. The cost of waiting wasn’t too bad. On the machine I programmed from 1978-1982, we didn’t even HAVE a CPU cache because it was only 12 cycles to access memory and each instruction took a handful of cycles. The lost work wasn’t too bad.
Now, we have amazing bandwidth from DRAM to processor caches. Each level of the cache is smaller but lower latency as you get close to the CPU core. Level-1 (close to the processor), Level-2 (shared across cores in a socket), and Level-3 (shared across sockets in a server) change in latency and size as they get closer to or farther from the CPU. Since multiple cores and multiple sockets may be writing the data while you are reading it, a lot of hardware is spent ensuring cache is coherent. This ensures each cache line of memory looks like a single-writer or multi-readers offering ordered (linearizable) reads and writes.
The more distant the sharing (e.g., across cores or across sockets), the more time we spend ensuring you have the correct version of data and the permission to write it. Write through caches ensure the latest value of the cache line is in the common shared cache. Invalidation caches leave the latest version close to the latest writer but need to go all the way to the last writer if someone else needs the cache line. Fighting over the permission to write a cache line can stall a core for many cycles. Over the years, the size of a cache line has increased as we hope to use more data within each cache line we’ve obtained. In my youth, fetching a 4-byte word was common on high-end systems. Now, we typically see 64-byte cache lines and I expect 128-byte cache lines will be common soon.
Modern CPUs separate instruction caches from data caches. Data caches have the fancy coherence hardware needed to allow coordination across many writers. Instruction caches leverage the assumption that instructions are read-only and don’t need coherence. Not surprisingly, recent machines are starting to have faster non-coherent data caches that can be used for many things but can’t be updated by more than one CPU at a time.
We are caching more and more data in DRAM just as we are caching more and more data within processor caches. This is because memory and bandwidth keep getting cheaper. It makes sense to keep data close.
Caching read-only data has many challenges. There are costs to shoveling read-only data around. There are costs to cache it. These costs continue to drop. Coordinating access to data that is NOT read-only is another kettle of fish entirely!
Inverting How We Write Data
Updating data in place is HARD. It’s even harder when the data is replicated across many servers in a cloud data center. Each step in the distributed systems dance for reliable update in place takes a LONG time.
Instead, we see a gradual increase in log-based solutions. LSM-Trees (Log Structured Merge Trees) work by writing new values for the keys they contain. Similar to an accountant’s ledger, the new entries take precedence over the old ones. With LSM, the system is constantly merging the new values (organized by their key) in the background to be close by other values with similar keys. This makes it easier to search for the latest value of the key. Frequently, old replaced values are eliminated in the new merged data.
LSMs spend bandwidth and computation reorganizing the data. They do this for a couple of reasons. First, updating data does not usually need to get its old value. That eliminates a round-trip. Second, by writing new data collections with unique-ids, the stored data is immutable. Massive sharing of huge amounts of immutable data is easy even across datacenters, servers, memory, and caches. See Immutability Changes Everything.
Increasingly, we organize our writes to only need a single round-trip to the distant storage. This log-based technique happens at MANY levels of the system. See Write Amplification versus Read Perspiration.
Coordination Is Getting More Difficult Relative to Other Things
What is NOT dropping is the cost to decide WHO can change data.
Sometimes, changes to a piece of data come from only one place. If there’s a single core making changes to a cache line just once and then ignoring it, the other cores (or sockets) can get read-access to those cache lines with a one-time coordination. The cores and sockets aren’t fighting and pulling back and forth. If one specific server in a cluster is the only truth behind a set of changes, the changes flow outward and other servers see what comes their way. That’s easier than coordinating; but WHO has the authority to change WHAT?
When thinking about the importance of new “No SQL” or Key-Value stores, we realize that this is a technique for the storage subsystem to partition or shard the coordination of changes. Each key and its storage server become a centralized focal point of change for its shard. We may have potentially long delays changing the “value” associated with a “key” as we talk to its owning node. What we avoid is a lot of time spent deciding which server IS the owning node.
Even more worrisome problems happen when we want our answers FAST. Most coordination scampers back to a centralized authority to get the truth. This may be accessing a centralized database or even accessing some consensus-based oracle like Zookeeper. To a very large extent, these centralized coordination points are vulnerable to long tail-latencies as they occasionally take a LONG time to do their job. Pretty much every centralized thing in a cluster occasionally takes a LONG time to do their job!
Some partial solutions to latency sensitive distributed logging are emerging. This is comparable to a blind write to a data location. Still, doing an authoritative coordination is neither fast nor does it usually offer flat tail-latency. This is a growing problem.
Happened Before: The Basic Idea Behind Our Work
Back in the day, we programmed within a single server; time didn’t seem too hard. As we moved from local programs with local main memory to distributed systems, we still look at the world through the prism of this very old model. In Leslie Lamport’s seminal paper Time, Clocks and the Ordering of Events in a Distributed System, he describes a notion of happened before. This defines a partial ordering of the events in a distributed system.
We still think in terms of order for most of our work. ACID transactions give the appearance of total order to the application running within the transaction. This is, in fact, only a partial order from the perspective of the database implementing the transactions. How do we maintain our subjective perspective of total order, preserving a sense of the happened before semantic and still reduce costs for the system to coordinate?
Partial order and happened before semantics provide a framework to defer coordination. We see this when the partial order is separated by disjoint space, by speculation over disjoint time, by separate abstraction layers, by replication and quorum, by versions and immutability, by confluence (where subsets of operations merge with monotonicity), by idempotence and functional calculation, and by equivalence within invariants. In many cases, these allow us to spend the resources we now find abundant to reduce our coordination.
Partial order defines a directed acyclic graph of order. Coordination happens when we coalesce two or more parallel arcs of the graph into one. Sometimes, that happens close in physical space and our computational memory hierarchy. In these cases, it’s less expensive to coordinate than when we coalesce parallel arcs that are far away. Partial order is, indeed, fractal as it branches and coalesces constantly.
The goal of coordination is to give the PERSPECTIVE of total order. When we coordinate, we combine two or more partial orderings into a larger ordering. The act of observing this larger ordering collapses many possible partial orders. What constitutes observation is a discussion in its own right.
We create partial orders within our system to make it possible to use our abundant CPU, memory, storage, and network. Can we spend more of these to avoid coordination and reduce the costs we’ve incurred as a consequence of these partial orders?
Tricks to Create and Coalesce Partial Orders
How do systems create partial order so they can minimize their coordination? This section will discuss a set of tricks that are commonly or not-so-commonly used to reduce coordination.
These are just some tricks that have popped to the top of my head. There may be more and I’d love to see a vibrant discussion about other possible tricks to avoid coordination and/or other ways to taxonomize these tricks.
Partial order from disjoint space
This is by far the most common way we avoid coordination. I’m pretty sure that we haven’t experienced significant problems coordinating with work running inside the Andromeda galaxy. It’s far away, their computation is disjoint from our computation, and there’s no need to coordinate. Our respective partial orders can live within a universe-wide global order without coordinating.
Indeed, it is reasonable to think of the universe as a close-to-infinite number of disjoint partial orders. Sometimes they interact and coordinate but mostly they don’t.
Linearizable chunks of space are the norm but not the rule. Back when our computers didn’t have networks connecting them, each computer had its own linearizable disjoint space. There was never an appearance of interactions across these computers because they weren’t connected! The recent trend to connect computers has caused a lot of confusion!
Linearizability is a property seen from the outside. When an outsider or outsiders interact with a linearizable thing, it looks like one operation at a time happens to the thing. Linearizability imposes a partial order on all operations invoked from outside the object. They look like they happen one at a time. It is important to remember that this says nothing about order across different objects being updated.
I would encourage everyone to carefully read Linearizability: a correctness condition for concurrent objects by Herlihy and Wing. I recently took the time to study it and found it a crisp and clear framing of the behavior of:
A single linearizable object and the operations that are performed on it, AND
A set of remote clients and the timing SEEN by these clients as they perform operations against this single linearizable object.
The operations on a linearizable object may or may not be simply read and write. A lot of folks tacitly assume this applies only to read and write operations!! It’s more general than that!
I sometimes lump a set of objects into collocated linearizable “chunk of space”. In this perspective, the set of objects must APPEAR to process operations from clients outside the “chunk of space” one operation at a time. Linearizability defines the timing and order as perceived inside the chunk of space as related to a bunch of clients outside the chunk of space.
Serializability breaks a larger linearizable space into multiple time-bound smaller spaces. Each of these has its own partial order. These smaller time-bound spaces are usually called transactions.
From the outside of a relational database (and its encompassing application), we can think of the entire database as having its own partial order with respect to everything else. From the outside, the database and its application SEEM to do one transaction at a time. From the outside of a database, it looks like it is linearizable!
This description assumes each application-encompassed-transaction LOOKS like a single operation to the outside. I know this is not always the case but when it IS the case, the operations do appear in a single linearizable order.
From the inside of the database, transactions look like a lot of concurrent things.
Serializability is a promise within the database.
Linearizability is an outside view of the application and database (if the application does a single transaction for each single application operation).
Both serializability and linearizability can be nested and hierarchical. Nested transactions provide a localized partial order within the partial order of the larger transaction. Nested transactions look like a linearizable sequence of changes from the perspective of the encompassing larger transaction. Indeed, sophisticated nested transactions (with nested isolation) can be serializable within the encompassing transaction. In turn, the larger transaction has a partial order within the database and this looks linearizable from outside the database.
Partial order from speculation and overlapping time
Sometimes, we allow a partial ordering of operations by allowing concurrent execution of work that may or may not survive to become visible to other stuff.
Fate sharing is a fascinating trick that binds one outcome to depend on another. It can ensure that one operation will cease to exist if an operation upon which it depends on ceases to exist. One common example of fate sharing can be seen in a group commit buffer for a transaction log. Typically, a later record in a log buffer cannot commit unless the first one commits. This may be used to allow the second transaction to use the data from the first one and not need to coordinate across the two transactions. Similarly, apparently sequential machine instructions in a CPU can avoid the cost of coordination by ensuring the second instruction cannot be visible outside the CPU unless both the first and second instructions are committed to memory. The second instruction shares the fate of the first one if it disappears.
Speculative execution allows parallel work that defers coordination. In modern CPUs, there may be hundreds of out-of-order instructions all calculating results that may or may not be seen outside the CPU. Most of these instruction executions are never seen but instead are discarded. Optimistic concurrency control in database systems is a form of speculative execution that defers coordination. While not common, it is entirely possible to have long sequences of transactions each dependent on their preceding transactions and devoting a LOT of work on the hunch that this sequence of changes will successfully change the underlying database when they finally coordinate with it. We can envision a large tree of uncommitted transactions each exploring possible paths into the future. Someday, databases may do this just like CPU chips have large trees of branch predictive speculative execution. This may defer coordination.
Immutable data coalesces speculation into fewer partial orders. Fewer partial orders mean you coordinate fewer times. When speculative execution runs over immutable inputs, there’s just one complete and correct outcome. This semantically avoids coordination. Indeed, if ALL of the data fed into some work is immutable, that work devolves (or evolves) into functional programming. Purely functional programming offers huge opportunities for avoiding coordination. All you need to do is prefetch the read-only data to bring it close to where it is needed. We see classic “big data” work leveraging immutable data and functional calculation at very large scale. Sub-components of large batch jobs may be idempotently retried without semantic implications to tolerate faults or slow execution.
Because the functional execution knows in advance what its inputs are, the consumer of the data need not compete for permission to change the data. There’s no tug-of-war over long distances to coordinate updates. You simply need a large enough truck to get the all input in one drive to the grocery store.
On the other hand, you can also speculatively execute on this immutable data before it is confirmed as useful. Coupling the fate of the OUTPUT from the new immutable dataset to the SUCCESSFUL CREATION of the previous immutable dataset can also reduce coordination.
Speculative execution and retries after timeout or failure are pretty much the same thing. In a purely functional programming environment (e.g., map reduce), the work is idempotent. You can do it as often as you want! Doing the work twice or thrice to avoid a timeout-and-retry avoids coordination. That is simply speculative execution. You spend computation to bound latency.
“Good enough” speculative execution is when parallel computation yields equivalent results. Of course, equivalence is in the eye of the beholder. We’ll talk more about that below. Retrying hedged requests within the search indices of a massive search system may give different answers when the replicas in a search index shard have different contents. They are usually “good enough”. See The Tail at Scale.
Partial order from layers of abstraction
Our complex systems comprise many different layers of abstraction. Avoiding side-effects across these layers of abstractions means we reduce coordination. Multiple partial orders don’t interfere on stuff that doesn’t matter. See Side-Effects, Front and Center!
Order is NOT NECESSARILY about read and write. Linearizability is a property of the order of operations against a single object which sees the operations in an order. If these operations are commutative, we can avoid a LOT of coordination! Commutative means “Seems like they’re ordered when they kinda aren’t ordered.”
Layers of abstraction can allow commutative operations that minimize coordination across partial orders. How these abstractions look to different parts of the system really depends on what you pay attention to and what you ignore. In general, ignorance is bliss; the less you know, the less you need to coordinate!
Layering abstractions to avoid interference. When working to allow parallelism across partial orders, we really want to order only the stuff we MUST order. When stuff that didn’t need to be ordered is, in fact ordered, we collapse partial orders into a larger ordering and incur coordination we didn’t need.
Inside a database, great care is taken to ensure that records from different transactions lying in the same database page don’t lock the page for the duration of the transaction. Older databases did this and it sucked. When lock conflicts impose ordering constraints that are not semantically required, we call those false conflicts. They suck.
Remote requests to micro-services hopefully don’t see interference due to the memory manager on the microservice. Leakage across layers of abstraction can introduce false conflicts that necessitate more coordination.
Commutative operations within a layer of abstraction can isolate partial orders. By allowing operations to be reordered, we avoid tying together the partial orders of the individual operations. This, in turn, can defer coordination until later and reduce the total coordination.
CRDTs (Conflict-free Replicated Data Types) allow for reordering of operations across transactions and replicas. This helps reduce coordination.
Escrow locking (see The Escrow Transactional Method – 1986) allowed commutative operations within transactions to avoid coordination across concurrent database transactions. Franco Putzolu and I built escrow locks for addition and subtraction into NonStop SQL in 1988. This helped our TCP-B benchmarks avoid contention and coordination on updates to the branch record. SQL’s addition/subtraction operators allowed us to avoid false conflicts inherent in read and write. We saw lots of concurrency of addition and subtraction by logging “+” and “-“ to describe the change. Hundreds of concurrent transactions could modify one “branch record” balance. It ran blazingly fast while you weren’t reading the balance. Reading the value took a while as it required that all outstanding transactions commit or abort before we allowed the read.
Abstracting equivalence within invariants is a powerful way to minimize coordination. One dollar is as good as the next so we don’t need exactly the same physical dollar bill. The count of available inventory may be encumbered by a reserved purchase. Still, we can track concurrent work on the inventory when it is commutative as long as we don’t run out. Our business MAY impose an invariant that we don’t sell more than we have. See Building on Quicksand.
A hotel may give you Room 301 as a king-sized non-smoking room declaring that it is equivalent to all other king-sized non-smoking rooms. This happens even if room 301 is next to the elevator and you get no sleep. Forcing many rooms into a common room type allows them to avoid coordination as they schedule room assignments.
Equivalence or fungibility may be subjective. It is not uncommon for me to think something is equivalent to something else while my wife disagrees with my assessment. Usually, she’s right.
“Equivalent” may not be equivalent as side-effects may kick in. You may fail to get your hotel reservation due to another guest’s reservation that is subsequently canceled. In this case, your partial order had unwanted coupling and coordination.
Are layers of abstraction really isolated particles or interacting waves? Just like in the Wave-particle duality in quantum mechanics, equivalence may be both! It appears to be a particle from the inside of the partial ordering of your work. Still, it may bump into other things outside your partial order that force premature coordination with other partial orders creating wave-like interactions. This may result in you staying in a crappier hotel.
Partial order: the disorder of input to confluent functions
Confluent functions are ones with a very special property. The order of their inputs does NOT impact the content of their outputs! Given the same set of inputs in any order, they produce the same set of outputs. This means we can remove order dependencies across the inputs and can, in turn, avoid COORDINATING THEIR ORDER! This works for some computations but not all.
It turns out that each confluent function is defined to have monotonic outputs. The function may NOT retract an output once it’s been produced. In many cases, confluent functions compose by allowing you to break up your work into multiple parallel confluent functions and merge their output. This makes it easy to compose a bunch of these confluent functions without coordinating across them! Just ship their partial work around, don’t worry about ordering or other annoying things. Over time, you gently cat-herd the completion of all the inputs.
Sealing a set of confluent functions happens when all inputs are KNOWN to have been processed. This DOES require coordination but hopefully, much less often as it happens only to seal a set of inputs.
The output of a confluent function that is still accepting inputs can answer a lot of questions in the category of “DOES EXIST”. If we’ve seen something in the output, it will remain in the output and hence, when we’re all done, it will still exist. In-flight confluent operations cannot answer a question about “DOES NOT EXIST” until their input is sealed. Only after we know all of the inputs have been processed AND we don’t see something in the output can we promise it won’t exist when we’re all done.
Future explorations of confluence to minimize coordination
Personally, confluence is a rather new concept for me. I’ve only been noodling over it and its relationship to sealing for a few years. There are MANY unexplored aspects to it and tons of opportunity to improve our distributed systems:
Ordering only matters when it matters. I’m especially intrigued by the combination of confluence with equivalence within invariants. If either of two partial orders is “good enough”, perhaps I never need to know which came first! Perhaps, the notion of which came first need not be resolved unless we look! Similar to the apocryphal “Schrödinger’s Cat”, both orders coexist until someone looks!
Confluent functions are monotonic. That means, the answer only gets better over time as more outputs are emitted. Suppose I have a collection of confluent functions that work to create travel arrangements for a trip. If my boss wants me to rapidly confirm that I can physically attend a meeting next Tuesday in Chicago, I may accept crappy travel arrangements to ensure I can attend. A network of confluent functions could start looking for plane, hotel, and car reservations sufficient to tell my boss I’ll be at the meeting. Even with center seats in a three-hop itinerary, I’ll be there.
After confirming my attendance, better and better travel options can arrive. Later in the afternoon, I may find out I can fly first class on a single-hop. Even later, I may learn about the better hotel close to the meeting. Each of these subsequent arrangements is better and, hence, even when spread over a complex graph of computation, new arrangements can monotonically improve without tight coordination.Subjective monotonicity. It’s important to remember that monotonic may be in the eye of the beholder! As we struggle to avoid coordination with new applications of confluent functions, we need to remember that one person’s opinion of “better” (i.e., monotonic) is not necessarily another person’s opinion! This epiphany is yet another wonderful advantage of being married.
Viewing Quorum as confluent operations
Voting quorums are fascinating and hard. We are all familiar with Gifford’s Algorithm that leverages weighted voting to ensure overlap of changes to a quorum set. Classically, we all say:
R + W > N
This is because we all assume that we are looking for the latest value (by reading it) and providing new values (by writing it).
When thinking of the quorum set as a collection of confluent functions, I have come to think about the more as:
O + I > N
If I provide INPUT to at least “I” replicas and grab OUTPUT as the union of “O” outputs from replicas, each input will be available as a part of the union of outputs.
If the operations on each replica within the quorum are reorderable, we are good! Accepting output from at least “O” replicas means I see all of the inputs. Since the order of the operations doesn’t matter, we can discern the complete result we need.
As a client wants to provide input, once “I” of the confluent functions (i.e., replica nodes in the quorum) have confirmed receipt of the operation, we can consider it durable. As long as there are MAX (I, O) replicas (or confluent functions) up and running, that fact will survive and be seen as output. Using that fact, we can completely answer “DOES EXIST” style questions.
Now, suppose these “N” replicas slowly and lazily gossip what they’ve learned. Each input item will, over time, be seen at all “N” replicas. That means, as-of the point in the past, we can view that old knowledge as sealed. This allows us to carefully answer questions about “DOES NOT EXIST”.
Garbage collection is a “DOES NOT EXIST” style problem. A file can only be garbage collected when we know a reference does not exist.
Consider an LSM that adds confluent knowledge of new files created by merging within the LSM. Old files are no longer needed when reads to the LSM don’t need the old file to produce the latest view of the keys in the LSM. If we are patient and only slowly garbage collect, we can base our decisions only based on facts known to be at ALL replicas. These replicas are gradually sealing historic input as they know the fact is visible at all replicas. Hence, we can base “DOES NOT EXIST” (e.g., garbage collection) on the set of inputs known to exist at all replicas.
Personally, there’s LOTS that I hope to learn about avoiding coordination with confluent functions!
Embracing Our Inner Uncoordinated Self
As we build ever more complex systems, we face increasing challenges avoiding coordination. This is important as the cost of coordination increases. We must really focus in on new techniques for integrating our stuff together.
Write is wrong! In general, we suffer from our old habit of using write as the basic operation for composition. What can we do to evolve away from this bad habit?
Life as an uncoordinated person is not so bad! It’s very rare for my wife to ask me to repair things around the house. Years of experience have taught both of us that it’s cheaper to call a repair person BEFORE I’ve made things worse.
Occasionally, I set out to do some change or make some repair to the house. Studying the instructions allows me to construct a planned partial order of operations on the components being installed and their subcomponents. Frequently, I clumsily drop a screw into the inside of the wall or break something. This results in my planned partial order of the repair not becoming part of the total order of the universe. This, in turn, ensures a repair person is called next time.
I’m SO glad I’m uncoordinated!
PS. Thanks to my friend and colleague, Jamie Martin, for encouraging me to write down what the hell I mean when I fuss and complain about coordination.
Open questions
We seem to be wedded to read and write as our model for work. How can we evolve away this self-abusive behavior and concentrate on WHAT we need rather than casting it as data items needing coordination?
Which is worse, READ or WRITE?
What is the best way to get long-term revenge on your coordinated schoolmates who excelled at sports and caught all the girls?
How can we get better at capturing equivalence and commutativity in our software primitives? If the Chicago Commodities Exchange can formalize “futures trading” of not yet existing pigs, (i.e., pork bellies) why can’t we teach programmers about equivalent and interchangeable things? Is it because programmers aren’t cool?
Why can’t we make speculative computation transparent for long-running workflows? Can’t we enhance performance while hiding all coordination from developers? It works inside CPUs, why not at a large scale?
Does this enumeration of anti-coordination tricks cover all we have? Surely, there must be more tricks up our sleeve to add to this taxonomy!
When will our culture advance far enough to see a LACK of coordination as a cool attribute?